Binary Numbers

When working with any kind of digital electronics it is important to understand that numbers are represented by two levels which can represent a one or a zero. The number system based on ones and zeroes is called the binary system (because there are only two possible digits). Before discussing the binary system, a review of the decimal (ten possible digits) system is helpful, because many of the concepts of the binary system will be easier to understand when introduced alongside their decimal counterpart.

Decimal System

You should all have some familiarity with the decimal system. For instance, to represent the positive integer one hundred and twenty-five as a decimal number, we can write (with the postive sign implied):

$$ 125_{10} = 1 \cdot 100 + 2 \cdot 10 + 5 \cdot 1 = 1 \cdot 10^2 + 2 \cdot 10^1 + 5 \cdot 10^0 $$

The subscript 10 denotes the number as a base 10 (decimal) number.

There are some important observations:

• To multiply a number by 10 you can simply shift it to the left by one digit, and fill in the rightmost digit with a 0 (moving the decimal place one to the right).
• To divide a number by 10, simply shift the number to the right by one digit (moving the decimal place one to the left).
• To see how many digits a number needs, you can simply take the logarithm (base 10) of the absolute value of the number, and add 1 to it. The integral part of the result will be the number of digits. For instance, \(\log_{10}(33) + 1 = 2.5.\)

Binary System (of positive integers)

Binary representations of positive integers can be understood in the same way as their decimal counterparts. For example

$$ 86_{10}=1 \cdot 64+0 \cdot 32+1 \cdot 16+0 \cdot 8+1 \cdot 4+1 \cdot 2+0 \cdot 1 $$

This can also be written as:

$$ 86_{10}=1 \cdot 2^{6} +0 \cdot 2^{5}+1 \cdot 2^{4}+0 \cdot 2^{3}+1 \cdot 2^{2}+1 \cdot 2^{1}+0 \cdot 2^{0} $$ or

$$ 86_{10}=1010110_{2} $$

The subscript 2 denotes a binary number. Each digit in a binary number is called a bit. The number 1010110 is represented by 7 bits. Any number can be broken down this way, by finding all of the powers of 2 that add up to the number in question (in this case \(2^6\), 2\(^4\), 2\(^2\) and 2\(^1\)). You can see this is exactly analogous to the decimal deconstruction of the number 125 that was done earlier. Likewise we can make a similar set of observations:

• To multiply a number by 2 you can simply shift it to the left by one digit, and fill in the rightmost digit with a 0.
• To divide a number by 2, simply shift the number to the right by one digit.
• To see how many digits a number needs, you can simply take the logarithm (base 2) of the number, and add 1 to it. The integral part of the result is the number of digits. For instance, \(\log_{2}(86) + 1 = 7.426.\) The integral part of that is 7, so 7 digits are needed. With \(n\) digits, \(2^n\) unique numbers (from 0 to \(2^n - 1\)) can be represented. If \(n=8\), 256 (\(=2^8\)) numbers can be represented (0-255).

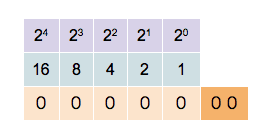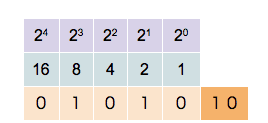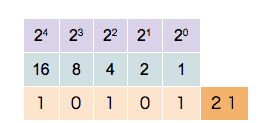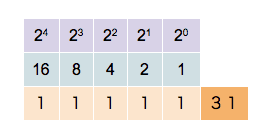
This counter shows how to count in binary from zero through thirty-one.